Ponto da situação
Há dois ou três posts atrás desenhei o esquema global que me propunha seguir. Acontece que vou tão "devagarzinho" e utilizando tantos atalhos que o leitor facilmente se poderá perder e não saber nem onde nem para onde vai.
Por isso resolvi iniciar cada post com uma espécie de índice, que vá indicando o ponto onde estamos.
Neste primeiro "capítulo", a ideia é chegar à primeira formulação do modelo de Big Bang e dar conta dos vários avanços e dificuldades. A vermelho o que já foi escrito; a negrito o tema de hoje:
1. Big Bang: (Sumário)
2. História milenar: Mitos da criação e começo da ciência com os gregos
3. Modelo geocêntrico e o aperfeiçoamento do Telescópio
4. Os avanços a partir de Copérnico (modelo geocêntico) e de Galileu (aperfeiçoamento da "medição")
5. Medição das distâncias astronómicas (Cefeidas)
6. Lei de Hubble, que apresenta provas experimentais da expansão do Universo
7. Modelos teóricos, que partem todos da Teoria da Relatividade
8. Modelo de Einstein
9. Modelo de Friedmann-Lemaître.
Antigamente só dispúnhamos dos olhos para ver o céu! Assim foram sendo feitas muitas observações, mas faltava "uma lei" que sistematizasse esses dados. Houve algumas tentativas, antes dos gregos, para explicar o Universo, como, por exemplo, esta proposta suméria.

Universo mesopotâmico
Mais uma vez foram os Gregos que tentaram respostas "racionais".
Empédocles (495-435 aC) procurou explicar a sucessão regular do dia e da noite com o "modelo de duas esferas" concêntricas: a interior era luminosa numa metade e transparente na outra, dando uma volta cada 24 horas; a exterior continha o firmamento, que era visível durante a noite, rodando uma vez cada 365 dias.

Modelo de duas esferas de Empédocles
Os gregos verificaram que havia uns corpos celestes que estavam mais ou menos fixos - as "estrelas fixas" - e outros que mudavam de posição - os planetas (πλανήτης, "errante, vagabundo").
Modelo Pirocêntrico (tem o fogo (piro-) no centro)
Para alguns, o primeiro a propor um modelo de Universo foi Filolau de Crotona, em meados do século V aC. Para outros, ele apenas teria sido o divulgador da doutrina pitagórica e do seu modelo de Universo.
Os Pitagóricos chamavam-se a si mesmos mathematikoi (Μαθηματικός, "os que estudam tudo; desejosos de aprender", que vem do verbo μανθάνω, "aprender, estudar" ). Esta palavra vem da raiz indo-europeia, men- que indica "movimentos do espírito", bem como mênis (μήνις), "ressentimento, ira", que é a primeira palavra da Ilíada e de algum modo justifica toda a acção:
Μήνιν άειδε, θεά, Πηληιάδεω Άχιλήος (Canta, ó deusa, a cólera de Aquiles, o Pelida).
Os Pitagóricos eram mais uma "irmandade", que confundia misticismo e "ciência", do que uma escola.
Para eles, a realidade era "matemática": os números são a essência da realidade. A partir deste pressuposto, era natural que o círculo fosse a forma mais perfeita.
O seu modelo do Universo não se trata de um modelo geocêntrico, mas pirocêntrico. A Terra não foi colocada no centro por razões de ordem moral e religiosa, já que, para eles, a Terra e tudo o que ela contém, incluindo a humanidade, era considerado imperfeito. Assim sendo, nunca poderia ocupar o centro, que é o local mais importante no Universo. Esse lugar especial estava reservado ao "Fogo Central", a "casa de Zeus", ou “motor” do Universo. Todos os astros giram em torno desse centro em órbitas circulares (símbolo da perfeição). As órbitas circulares mantiveram-se durante dois milénios. O modelo contava ainda com uma Anti-Terra (Antichthon de chthon (χθών), "terra", que aparece na nossa palavra autóctone) não só para que o número de astros fosse dez mas também para evitar que a Terra visse o Fogo Central. Para isso, a Anti-Terra girava de tal modo que ficava sempre entre a Terra e o Fogo Central.
É curioso que foram os números que de algum modo vieram pôr em causa os fundamentos dos Pitagóricos. Coisa aparentemente mais simples não poderia ser, mas pôs em causa essa ubiquidade numérica: a raiz quadrada de dois. Geometricamente é evidente que a raiz quadrada de dois existe.
Basta aplicar o "teorema de Pitágoras" (que ele teria herdado dos babilónicos!?) ao triângulo acima. A hipotenusa é exactamente "a raiz quadrada de dois". Mas quanto vale numericamente? Não é possível saber, mesmo hoje, porque se trata de um "número irracional", isto é, não se pode obter pela divisão de dois números inteiros. Podemos calculá-lo com vários milhões de decimais. Aqui ficam os primeiros 75
√ 2 ≈ 1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462...
Terá sido Hipaso de Metaponto (que teria nascido no ano 500 aC), um seguidor de Pitágoras (de 570-497 aC), que teria demonstrado que se tratava de um número irracional. No entanto, Pitágoras considerava que a raiz de 2 "maculava" a perfeição dos números e, portanto, não poderia existir. A lenda diz que, não tendo conseguido refutar os argumentos de Hipaso com a lógica, Pitágoras condenou-o ao afogamento. Terá mesmo de ser uma lenda, pois quando Pitágoras morreu, Hipaso teria 3 anos!
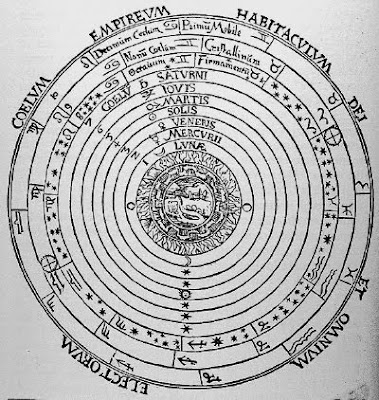
Modelo(s) Geocêntrico(s)
Dois discípulos de Platão propuseram dois modelos diferentes.
O modelo de Aristóteles (384-322 aC) mistura os elementos, que formam toda a matéria, os planetas e as estrelas fixas: no centro a Terra é formada por terra com uma camada exterior de água - os mares - sobre a qual havia uma camada de ar - a atmosfera - e outra de fogo que termina na esfera da Lua, à qual se seguem as esferas do Mercúrio, Vénus, Sol, Marte, Júpiter, Saturno (os únicos cinco planetas conhecidos até ao século XIX) e finalmente a esfera das estrelas fixas. Aristóteles aproveitou a concepção geométrica pitagórica de um modelo esférico, simples e harmonioso, mas retirou as características mitológicas, introduzindo uma alteração substancial: colocou a Terra no centro, dando assim origem ao geocentrismo.
Modelo geocêntrico de Aristóteles
Aristóteles não concordava com o seu mestre Platão. Enquanto este insistia no fundamento matemático da natureza, Aristóteles defendia que o mundo seria melhor compreendido através da sua observação. S. Tomás de Aquino sintetiza bem esta ideia numa célebre frase que decorei nos meus tempos de Seminário: Nihil est in intellectu quod non fuerit prius in sensu: "Nada existe no intelecto se antes não tiver estado nos sentidos". Não sei se teve alguma influência, mas o poeta grego Alcmane, do séc. VII AC, tem uma afirmação que, sendo mais lata, tem subjacente uma ideia semelhante: Пεῖρά τοι μαθήσιος ἀρχά: "A experiência (experimentação!?) é a base do conhecimento".
Mas o método científico de Aristóteles não deve ser entendido como hoje. Ele olhava o mundo "à distância" e tirava as suas conclusões. Não sujava as mãos na experiência. O caso mais paradigmático e anedótico era a sua afirmação de que homens e mulheres tinham um número diferente de dentes! Ora, bastava tê-los contado para verificar que assim não era!
O método de Heráclides (388-315 aC) surge para responder às dificuldades do sistema geocêntrico em explicar os movimentos dos planetas com relação às estrelas fixas. Trata-se de um sistema misto em que a Terra "continuava" no centro do Universo, mas Mercúrio e Vénus orbitavam em torno do Sol, até porque eram sempre vistos muito próximos dele. Defendeu também a ideia de que a Terra rodava sobre si própria demorando um dia, o que explicava o movimento diário de todos os astros. Já Hicetas (400-335 aC) propusera que a Terra girava em torno de um eixo.
Este foi o primeiro de muitos ajustamento a que o modelo geocêntrico foi sujeito para melhor responder às observações que iam sendo feitas.
Mas o modelo mais famoso deve-se a Ptolomeu (120-180 dC). É geocêntrico, com órbitas circulares e com uma esfera exterior com as estrelas fixas.
O movimento dos planetas era explicado de um modo algo complexo: os epiciclos. O que roda em torno da Terra, não é o planeta, mas um ponto chamado Deferente. E é em torno desse Deferente que o planeta descreve a sua órbita, o Epiciclo.

Mas Ptolomeu resolveu aperfeiçoar (complicar) ainda mais o seu modelo, colocando a Terra numa posição um pouco afastada do Centro do Deferente (portanto o Deferente é um círculo excêntrico em relação à Terra). E, para explicar o movimento não uniforme dos planetas, introduziu um novo ponto, o Equante, que fica simétrico à Terra em relação ao Centro do Deferente, e em relação ao qual o centro do epiciclo se move a uma velocidade constante.
Possivelmente Ptolomeu foi buscar a ideia dos epiciclos ao matemático e astrónomo grego Apolónio de Pérgamo (262 a 190 aC), chamado o Grande Geómetra, que melhorar o modelo de Eudoxo de Cnido (390 a 337 aC).
Recordei tudo isto, para dar conta da complexidade do modelo, que conhecemos como muito simples, e saudar todo o trabalho de várias gerações para obterem um modelo cada vez mais capaz de responder ao que realmente se passava na natureza.
E já agora, como mera curiosidade apresento aqui um desenho de modelo ptolomaico feito pelo cosmógrafo e cartógrafo português Bartolomeu Velho (?-1568), publicado no seu livro Cosmographia (França, 1568). A sua novidade é que do lado esquerdo indica as distâncias ao centro da Terra e do lado direito a duração, em anos, da translação dos vários "planetas".
Trajectória do centro de massa do Sistema Solar
Só mais uma complicação final.
Rigorosamente o Sol não está no centro (ou foco) mas ele próprio orbita em torno do centro de massa (baricentro) do Sistema Solar. Num post anterior já expliquei que, quando um corpo gira em torno de outro, nenhum está totalmente fixo. Ambas giram em torno do centro de massa, ponto que está tanto mais próximo do centro do maior quanto maior for a diferença das suas massas.
Pois também o Sol, apesar de conter a quase totalidade da massa do Sistema Solar (99,86% ), orbita, como todos os planetas, em torno do centro de massa do Sistema Solar. O movimento é muito complicado por causa das perturbações gravitacionais dos oito planetas e também outros corpos.
Mesmo depois da Idade Média, aparecem gravuras com o modelo geocêntrico, apesar de já ter sido demonstrada a sua falsidade.
Mas a imagem mais famosa foi publicada por Camille Flamarion, representando a curiosidade humana para saber o que haverá para lá do visível, das "estrelas fixas".
TELESCÓPIO
O grande impulso para a astronomia veio do Telescópio, que tem uma longa história atrás.
Desde a antiguidade povos como os egípcios, gregos e romanos conheciam a arte de talhar e polir cristais de rochas e usam essas primeiras lupas primitivas como objectos decorativos. Não se sabe ao certo quando as lentes foram inventadas. A notícia mais antiga aparece, em 721 aC, na referência a um cristal de rocha recortado com propriedades de ampliação. Não encontrei a localização de tal inscrição.
Os chineses já dominavam a arte de produzir lentes simples a partir de cristais de quartzo e outros materiais, com armações de diferentes materiais, como o carey, retirado das escamas da tartaruga . Alguns destes "óculos" tinham finalidades ornamentais e medicinais. Confúcio (500 aC) diz ter aliviado a visão de um sapateiro com o uso de lentes. Marco Polo, na visita à China, em 1270, encontrou pessoas que usavam aqueles ornamentos. O imperador Nero usava pedras preciosas para ver melhor os actores em palco.
Os primeiros óculos foram fabricados por Salvino D'Armato em 1285, conforme se lê na sua inscrição funerária: "Aqui jaz Salvino D'Armato de Amati de Florença. Inventor dos Óculos. Deus perdoe os seus pecados. A. D. 1317". Há, no entanto, quem atribua a sua invenção ao monge Alejandro Spina, que, nos meados do século XIII, divulgou o segredo e a construção da fabricação de lentes correctivas.
Depois da sua invenção, os óculos rapidamente se popularizam e logo começaram as primeiras experiências de combinação de lentes para aplicação em instrumentos de ampliação de imagens, resultando na criação do primeiro microscópio composto (duas ou mais lentes).
Nos finais do século XVI, os italianos descobriram novos métodos de produção de vidro, o que permitiu a associação de lentes. Mas foi o holandês Hans Lippershey que, em 1608, patenteou a descoberta do telescópio, quando, ao olhar através de duas lentes, viu a torre da Igreja ampliada. Porque usava lentes, tratava-se de um telescópio refractor. Diz-se que fez a descoberta quando ensinava os miúdos a brincar com duas lentes.
Parece que o primeiro utilizador do telescópio em astronomia poderá ter sido Thomas Harriot (1560 - 1621): as suas observações datam de Agosto de 1609. Foi também o primeiro tentar mapear a Lua (mapa que ficou inédito até 1965) e a observar manchas solares, em Dezembro de 1610.

Harriot: Mapa da Lua e Manchas Solares
Mas foi J. Fabricius quem primeiro publicou as suas observações, ainda em 1611, no seu livro De maculis in Sole observatis, livro, que permaneceu desconhecido por algum tempo. Entretanto Galileu deu a conhecer as suas observações em Roma.

Manchas solares descritas por Fabricius
Mas o conhecimento das manchas solares já tinha uma longa história. A referência mais antiga foi feita pelo chinês Gan De em 364 aC. A primeira menção na literatura ocidental é de 17.Março.807 dC e deve-se ao monge beneditino Adelmus, que observou uma mancha tão grande que foi visivel durante oito dias. Uma outra foi visível por altura da morte de Carlos Magno (28.Janeiro.814). A actividade das manchas solares, em 1129, foi registada por John of Worcester.

Descrição da actividade solar em 1129
De qualquer modo,é com Galileu que o telescópio se divulgou e se tornou um instrumento cada vez mais indispensável à astronomia.
Luneta de Galileu
É formada por duas lentes: a objectiva, biconvexa de grande distância focal, e a ocular, divergente de pequena distância focal e pequeno diâmetro, colocadas de modo a que os Focos coincidissem no mesmo ponto.
Os raios luminosos entram na objectiva, colocada na frente do tubo, e convergem até ao Foco. Mas antes passam pela ocular que dá uma imagem não invertida e maior que o objecto.
Aperfeiçoando as lentes conseguiu uma ampliação de 20 vezes. Falarei no próximo post das suas “descobertas”.
Luneta de Kepler
Em 1611, Kepler introduziu uma alteração: é formada também por duas lentes, mas ambas convergentes.
A trajectória dos dos raios luminosos é semelhante à que acontece na luneta de Galileu, mas os raios convergem antes de atingir a ocular, que fornece uma imagem maior e invertida do astro observado.
Portanto, contrariamente à de Galileu dá uma imagem invertida pelo que se usa apenas em observações astronómicas.
As lentes, no entanto, apresentam um problema chamado aberração cromática (ver mais abaixo). Para limitar este problema, as lentes tinham de ter um pequeno grau de curvatura, ou seja, uma distância focal muito grande, o que obrigava a telescópios muito longos. O maior talvez tenha sido o de Hevelius, com 42 m de comprimento, enquanto o de Galileu tinha entre 1,5 a 2 m.
Com este telescópio, Hevelius fez um mapa pormenorizado da Lua com 286 crateras, montanhas, “mares”.
Telescópio de Reflexão
Newton (1643 -1727), pensando que nenhuma lente poderia resolver o problema da aberração cromática, inventou o telescópio de reflexão, substituindo as lentes por espelhos, já que espelho reflecte todas as cores de modo igual e, portanto, não sofrendo de aberração cromática.
No seu telescópio, a imagem, focada pelo espelho primário esférico ou parabólico, é desviada por um espelho secundário (plano) colocado a 45º, para observação através da ocular, perpendicular ao tubo do telescópio.
Em 1672, o francês Cassegrain introduziu uma alteração, que vigorou até hoje: um espelho secundário, convexo, reflecte a luz que lhe incide, para trás do espelho principal, passando por um orifício existente no seu centro, formando a imagem atrás do espelho principal.
Solução para a Aberração Cromática
O problema da aberração cromática foi resolvido por John Dollond (1706 - 1761), oculista inglês, por meio de uma combinação adequada de lentes.
Este fenómeno deve-se ao facto de a luz ser formada por várias cores que. ao passarem pelo bordo de uma lente, são desviadas de modo diferente. Dollond resolveu acoplar duas lentes, com coeficientes de refracção diferentes (uma lente convergente de cristal leve e outra lente divergente de cristal pesado) para compensar a aberração cromática efectuada por uma só lente, inventando a lente acromática, hoje usada nas objectivas das máquinas fotográficas e cinematográficas, microscópios, telescópios.
Para trabalhos de elevada qualidade, a correcção acromática é feita com lentes compostas de três ou mais tipos de vidro, constituindo as objectivas chamadas apocromáticas, popularmente conhecidas como "processadas".
TELESCÓPIOS DO FUTURO
E agora uma brincadeira. Dois telescópios previstos para estarem a funcionar lá para futuro a médio prazo.
O Hipertelescópio SKA (Square Kilometre Array) vai estender-se por um círculo de 3000 km de diâmetro (da Austrália à África do Sul). Será formado por 3000 antenas parabólicas e 250 conjuntos de antenas compactas, com a forma de cinco braços espiralados. Quando estiver a funcionar em pleno, lá para o ano 2020, o volume de dados recolhidos será 200 vezes maior que o actual volume de dados mensal da Internet.
A área total de recolha de dados terá aproximadamente 1 km2, daí o seu nome “square kilometer”. Será 50 vezes mais sensível e terá uma velocidade de análise (survey) de dados dez mil vezes superior aos melhores telescópios actuais.
O seu objectivo é responder a perguntas fundamentais sobre o Universo: como se formaram as primeiras estrelas e galáxias pouco depois do Big Bang, como evoluíram desde então, qual o papel do magnetismo no Universo, qual a natureza da gravidade. E ainda vai à procura de vida extraterrestre.
Fonte: Expresso de 15.Maio.2010
O Hipertelescópio EEI (Exo Earth Imaginer) será constituído por por 10 000 espelhos de 3 m que formarão uma esfera no espaço com 400 km de diâmetro, no centro da qual estará um satélite recheado de aparelhos que sintetizarão as imagens e os dados e depois de processados os enviarão para a Terra. Terá uma ampliação de cem milhões de vezes, o que lhe permitirá identificar sobre os exoplanetas (planetas de outros sistemas solares) formações atmosféricas, continentes, cadeias montanhosas, variações sazonais, etc..
Fonte: Science et Vie Hors Série nº 239 (Junho.2007), p. 77























Sem comentários:
Enviar um comentário