1. Big Bang (Sumário)
2. História milenar (Mitos da criação e começo da ciência com os gregos)
3. Modelo geocêntrico e o aperfeiçoamento do Telescópio
4. Teólogos, filósofos, poetas e astrónomos em debate
5. Máquina do Mundo (Lusíadas, Canto X)
6. Descobrimentos e a "ciência" (1)
7. Descobrimentos e a "ciência" (2)
8. Descobrimentos e a "ciência" (3)
9. Os Lusíadas: significado da epopeia
10. As "contra-epopeias"
11. A caminho do modelo heliocêntrico
12. O génio do "método experimental" (Tycho Brahe e Kepler)
12A. O génio do "método experimental" (Tycho Brahe e Kepler)
13. O génio do "modelo experimental" (Galileu) – Descobertas
14. Caso Galileu (1)
15. Caso Galileu (2)
16. A caminho das estrelas
17. Primeiras medições astronómicas
18. Medição das distâncias: Descoberta das Cefeidas
19. Medição das distâncias: a Fotografia entra em cena
20. Medição das distâncias: Cefeidas como Padrão de Medida
21. Interregno: Mini-Guiness sobre as Estrelas
22. História da Luz: Olho
23. História da Luz
24. Luz e Espectroscopia
25. Problema das Galáxias
26. Medição da velocidade das
galáxias (Efeito de Doppler)
27. Lei de Hubble
28. Modelos teóricos partem todos da Teoria da Relatividade
Vimos
no último post, como através da espectroscopia se podia determinar a composição das
estrelas e outros astros celestes.
Hoje
vou mostrar como a mesma espectroscopia permite medir a velocidade com que
esses corpos de deslocam: se se aproximam ou se se afastam de nós e a quantos
quilómetros por segundo.
Esta
medição é possível através do conhecido efeito Doppler
EFEITO DOPPLER
Este
fenómeno está bastante presente na natureza, embora só “muito tarde” tenha sido
estudado.
Um
dos exemplos mais simples é dado pela deslocação de um cisne na água. Aparece
bastante distorcido. Mas como tudo na vida, nada é perfeito; nada é preto ou
branco: é sempre uma mistura. O mesmo se pode dizer de um navio em
deslocamento.
Este efeito é uma característica observada em
ondas emitidas ou refletidas por fontes em movimento relativo ao observador.
Foi descrito cientificamente pela primeira vez em 1842 por J.Ch.A. Doppler,
(daí o seu nome), que verificou que o movimento de um qualquer objecto afecta
as ondas que produz, quer se trate de ondas aquáticas, sonoras ou luminosas.
Dito por outras palavras. Basta comparar a variação do espaçamento das ondas para saber se o objecto emissor se aproxima ou se afasta.
Esta pode ser a definição geral do efeito Doppler: se o comprimento de onda é menor que o observado em repouso, o objecto está a aproximar-se; se é maior, está a afastar-se.
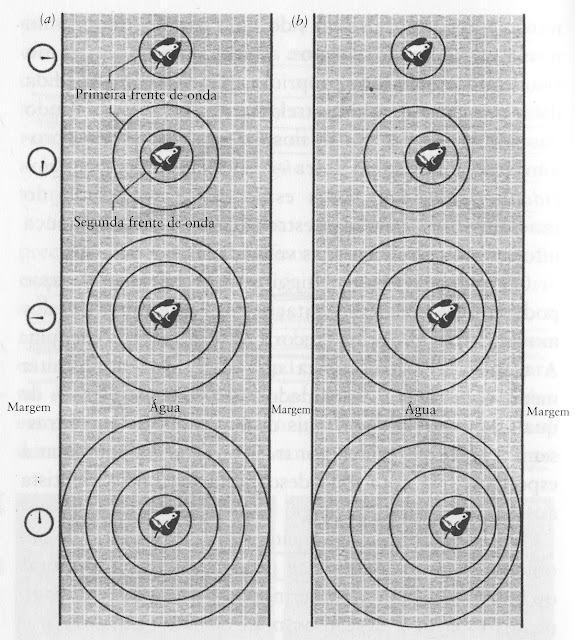
Efeito Doppler na Água
Imagine-se
uma rã a descansar numa pequena pedra no meio e um lago circular. E imagine-se
que a rã bate com a pata na água uma vez por segundo. O resultado é a formação
de ondas concêntricas que se deslocam à velocidade de, suponhamos, 1m/s. Os
observadores, em lados opostos, verão chegar as ondas com intervalos de 1m.
Porém,
se a rã saltar da pedra e se puser em movimento para o lado do observador da
direita, continuando a bater as patas ao mesmo ritmo e deslocando-se a 0,5 m/s,
verifica-se que as ondas ficam mais juntas para o lado em que se deslocam e
mais afastadas no sentido oposto.
Fonte: Simon Sang, Big Bang, p. 276
O
observador da direita vê, portanto, as ondas chegarem com intervalos de 0,5m
enquanto para o da esquerda o espaçamento das ondas é de 1,5m. É nisto que consiste
o efeito Doppler: as ondas comprimem-se quando se aproximam e distendem-se
quando se afastam.
Efeito Doppler no Som
O meteorologista holandês Ch. Buys-Ballot não acreditava na existência deste Efeito. Para provar a sua tese imaginou uma experiência bastante original. Contratou dois grupos de corneteiros a quem pediu que tocassem o mi bemol.
Mandou um para um comboio em andamento e outro ficou na gare.
Desta
experiência tirou duas conclusões:
1)
Quando o comboio se aproximava da gare, um ouvido apurado verificava que o som
se tornava mais agudo e quando se afastava, o som tornava-se mais grave. Afinal, o efeito Doppler era real. Isto é, obteve o resultado que provava a a existência do que ele pensava que não existia.
2)
Esta mudança no som era tanto mais acentuada, quanto maior a velocidade do
comboio. Convém recordar que esta mudança de tom se deve a mudanças do
comprimento de onda das ondas sonoras.
Hoje,
os exemplos mais usados são os de uma ambulância a apitar ou o da passagem de
um comboio. E para os amantes do automobilismo ou do motociclismo, as corridas desportivas são
também um óptimo exemplo para quem está, como eu, a ver uma corrida na
televisão, sentado num sofá. A mudança do som mais agudo para o mais grave é
claramente audível nestes três exemplos, quando a fonte emissora de ruído passa
por nós.
Podemos fazer um cálculo aproximado da variação
do comprimento de onda (λ) da sirene de uma ambulância, servindo-nos da equação deduzida por Doppler.
Se
uma ambulância se deslocar a 100 km/h, a variação do λ da
sirene desta ambulância era de cerca de 10 %
Estampido Sonoro
Quando
a velocidade da fonte é superior à velocidade do som (340 m/s ou Mach 1), dá-se
um fenómeno chamado “estampido som”, a que corresponde realmente um barulho
muito forte quase explosivo, causado pelo facto de o objecto bater e ultrapassar
a “barreira do som”. Esta explosão acontece porque quando a velocidade de um
objecto se aproxima de Mach 1, as frentes de onda começam a comprimir-se,
acabando por se sobrepor. Quando a velocidade se torna superior à do som
produz-se um cone (“conificação”) de ondas que se “atrasam” e que é o
responsável pelo estampido.
O
exemplo mais conhecido passa-se com os aviões supersónicos. O ruído, que pode
exceder os 200 decibéis, é devido à enorme energia dissipada que inclusivamente
produz a condensação da humidade que rodeia o avião.
Um
avião F/A-18 Hornet, ao passar a abarreira do som, produz um disco branco de
vapor de água condensada pela onda de choque.
Mas
também já aconteceu que, por problema de estrutura, o avião não suporte a
pressão e acabe por explodir, como se verificou, a 20.Set.1995. No vídeo tirado do porta-aviões, vê-se primeiro a formação da nuvem de vapor, depois uma
segunda nuvem de vapor e finalmente a explosão do avião.
Fenómeno do dia a dia
Aliás, este fenómeno não acontece apenas com aviões, mas também em muitos fenómenos da vida corrente. Por exemplo, quando se sacode uma toalha para a limpar de migalhas com suficiente rapidez, ouve-se um pequeno estampido sonoro. Mais conhecido é o estampido sonoro do chicote do domador de leões num circo. Se o chicote se movimentar mais rapidamente que o som, haverá um estampido sonoro em miniatura e se nas proximidades houver uma mesa cheia de pó poder-se-á ver o pó a espalhar-se como no caso do avião acontece com a humidade.
Aliás, este fenómeno não acontece apenas com aviões, mas também em muitos fenómenos da vida corrente. Por exemplo, quando se sacode uma toalha para a limpar de migalhas com suficiente rapidez, ouve-se um pequeno estampido sonoro. Mais conhecido é o estampido sonoro do chicote do domador de leões num circo. Se o chicote se movimentar mais rapidamente que o som, haverá um estampido sonoro em miniatura e se nas proximidades houver uma mesa cheia de pó poder-se-á ver o pó a espalhar-se como no caso do avião acontece com a humidade.
O
próprio trovão é também um estampido sonoro produzido pelo aumento de
velocidade do ar aquecido pelo relâmpago.
Efeito Doppler na Luz
A velocidade das
estrelas em relação ao Sol pode ser decomposta em várias componentes de que irei referir apenas duas: o movimento próprio e a velocidade radial.
Movimento próprio
Antes
de revolução copernicana, as estrelas, supunha-se, eram fixas: ocupavam a
última esfera, fixa. Desde Galileu, os astrónomos supunham que as estrelas eram
estacionárias. Todos viam que elas mudavam de posição durante a note, mas
sabia-se que esse movimento era aparente, devido à rotação da Terra.
Contudo, em 1718,
Edmund Halley demonstrou que não era bem assim. Observou algumas discrepâncias
(http://astro.if.ufrgs.br/vialac/node4.htm) nas posições das estrelas Arcturus
(1º) e Sirius (0,5º) relativamente às posições registadas por Ptolomeu (85-165
dC) e atribuiu-as não a erros de medição, mas a mudanças reais das estrelas.
Desde
então, os astrónomos têm medido este movimento transverso, chamado movimento próprio, perpendicular à
linha de visão. É difícil de detectar (mede-se em segundos de grau por ano), pelo
que exige a observação das estrelas mais próximas ao longo de vários anos. De
um modo simplista, pode comparar-se ao movimento dos planetas em torno do Sol.
No caso das estrelas, trata-se de um movimento em torno do centro galáctico da
ordem dos 200 km/s,
o que dá ideia da sua pequenez. Veja-se, a título de exemplo, a evolução da
constelação Cruzeiro do Sul, em três posições separadas por 50 000 anos:
Conhecem-se
apenas 35 estrelas com movimento próprio superior a 3 segundos de grau (”) por
ano. A que apresenta o maior valor é a estrela de Barnard 68, descoberta em 1916:
10,13” por ano.
O
traço contínuo é o movimento próprio da estrela medido pelo satélite Hiparcos.
A oscilação da estrela em torno desta recta é devida à paralaxe, isto é o
resultado ou reflexo do movimento de translação da Terra em torno do Sol.
Dada
a grandeza do seu movimento próprio, a sua evolução é bem visível ao longo dos
anos
Velocidade Radial
No entanto,
não é este o movimento que mais nos interessa. O que é importante é a velocidade radial, isto é, a velocidade
com que se aproxima ou se afasta da Terra.
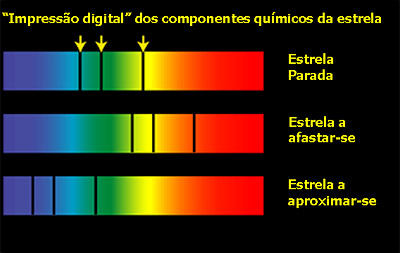
De qualquer
maneira o princípio é o mesmo: quando há aproximação, as ondas comprimem-se, o que
corresponde a desviar a cor para o lado azul; quando o objecto se afasta, há um
desvio para o vermelho, muitas vezes conhecido pela expressão inglesa redshift.
A mesma estrela aparece mais azulada quando se aproxima (observador do lado esquerdo) e mais vermelha quando se afasta (observador do lado direito)
Esta
deslocação da estrela repercute-se, portanto, na posição das riscas espectrais
que dos elementos que formam a estrela. Quando a estrela está em movimento, as
riscas espectrais aprecem desviadas da sua posição “normal”, isto é, quando
estão em repouso. Ou neste caso, quando o espectro é tirado no laboratório.
Tal como
calculámos a variação do comprimento de onda da sirene também podemos calcular
a variação do comprimento de onda da luz da ambulância. Nas mesmas
circunstâncias, a variação é muito menor: 0,00001%. Portanto demasiado pequena
para ser detectada pelos olhos humanos. Por isso, foi necessário esperar por
telescópios apropriados para detectar tão diminutas diferenças.
Situação especial
Se uma galáxia ou uma estrela ou mesmo um planeta têm o seu plano de rotação alinhado com a Terra o seu espectro apresenta uma configuração curiosa: o espectro tirado na zona que se aproxima de nós aparece com as riscas desviadas para a extremidade azul; o que é tirado da zona que se afasta de nós apresenta as riscas deslocadas para a extremidade vermelha.
É o caso da galáxia NGC 7541, que se vê na imagem abaixo, à esquerda. Do lado direito vemos o espectro. A parte superior está a aproximar-se de nós, portanto as riscas estão desviadas para a direita e tanto mais quanto maior é a sua velocidade: a "extremidade" A da galáxia é a que anda a maior velocidade e, portanto a risca correspondente a A está um pouco mais deslocada para a direita que B, zona da galáxia que gira a uma velocidade menor. Na parte inferior acontece o inverso: em C, a outra "extremidade" da galáxia, é que acontece o maior desvio, mas agora para a esquerda (azul) porque essa zona está a afastar-se de nós. Em D, o desvio é também para o azul mas em menor quantidade.
É devido à rotação sobre si própria que cada metade da galáxia nos envia espectros deslocados em sentidos diferentes: a de cima gira apontando para nós, isto é, está a aproximar-se, enquanto a de baixo gira afastando-se de nós.
Situação especial
Se uma galáxia ou uma estrela ou mesmo um planeta têm o seu plano de rotação alinhado com a Terra o seu espectro apresenta uma configuração curiosa: o espectro tirado na zona que se aproxima de nós aparece com as riscas desviadas para a extremidade azul; o que é tirado da zona que se afasta de nós apresenta as riscas deslocadas para a extremidade vermelha.
É o caso da galáxia NGC 7541, que se vê na imagem abaixo, à esquerda. Do lado direito vemos o espectro. A parte superior está a aproximar-se de nós, portanto as riscas estão desviadas para a direita e tanto mais quanto maior é a sua velocidade: a "extremidade" A da galáxia é a que anda a maior velocidade e, portanto a risca correspondente a A está um pouco mais deslocada para a direita que B, zona da galáxia que gira a uma velocidade menor. Na parte inferior acontece o inverso: em C, a outra "extremidade" da galáxia, é que acontece o maior desvio, mas agora para a esquerda (azul) porque essa zona está a afastar-se de nós. Em D, o desvio é também para o azul mas em menor quantidade.
É devido à rotação sobre si própria que cada metade da galáxia nos envia espectros deslocados em sentidos diferentes: a de cima gira apontando para nós, isto é, está a aproximar-se, enquanto a de baixo gira afastando-se de nós.
É também o que acontece com esta hipotética estrela.
É finalmente o que acontece com o planeta Saturno.
Efeito Doppler
Relativístico
Esta
historieta permite-nos falar de um fenómeno semelhante ao do estampido do som. Para
podermos notar realmente uma mudança visível da cor, a fonte da luz tem de
deslocar-se a uma enorme velocidade, chamada relativística, pois têm a ver com
exigências decorrentes da Teoria da Relatividade. Por isso se chama também a
este fenómeno Efeito Doppler Relativístico.
Há, contudo uma diferença relativamente ao som: a fonte emissora da luz nunca
poderá ultrapassar, como é óbvio, a velocidade da luz.
Mas
vejamos o que vê um observador quando se verifica um aumento de velocidade da
fonte luminosa.
O ponto azul representa o observador e
a seta, a velocidade do observador. Quando o observador está parado, a grelha aparece amarela. O aumento da velocidade do observador para a direita altera as
cores e a "aberração da luz" distorce a grelha. Quando o observador olha para a frente
(lado direito da grelha), os pontos vão tomando as cores verde, azul e violenta
(blueshift, desvio para o azul, porque o observador está a aproximar-se) e as linhas da grelha parecem mais
distantes. Se o observador olha para trás (lado esquerdo da grelha), então os
pontos parecem vermelhos (redshift, desvio para o vermelho, porque o observador está a afastar-se) e as linhas mais juntas.
Resumindo: Como afirmara Doppler logo no seu primeiro artigo, o efeito Doppler acontece com qualquer tipo de ondas, aquáticas, sonoras ou luminosas.
MEDIÇÃO DA VELOCIDADE DAS NEBULOSAS
SILÊNCIO que se vai tocar... o Effect Doppler
E para terminar ouçamos esta peça da compositora norte-americana Adrienne Albert, nascida em 1941, intitulada "Efeito Doppler". Ela própria conta como lhe surgiu a ideia: "A ideia de escrever uma peça, baseada nas constatações de um matemático austríaco que observou o aumento e a diminuição da altura do som quando a fonte e o observador se aproximavam ou se afastavam, surgiu-me durante uma viagem a Itália, ao ouvir as miríades de sirenes passando pelo meio de um trânsito tão intenso. O motivo (da peça) desce por uma segunda menor, retornando à harmonia original combinada com as segundas menores repetidas, retratando os sons incessantes das buzinas dos carros. As linha smelódicas retratam a vitalidade e a sensualidade das pessoas em contraste com a loucura que se passava em torno delas".
Efeito Doppler com os três tipos de ondas
Fonte: Maria Helena Dias da Silva et alt.,Velhos Rumos Caminhos Outros (Química A 10º ano), p.96
MEDIÇÃO DA VELOCIDADE DAS NEBULOSAS
William Huggins, como vimos no post anterior, obteve os primeiros espectros de estrelas em 1863. Na sequência de um rigoroso programa de experiências fotográficas em astronomia, a sua esposa Margaret deu uma primeira entrada, relativa a Sirius, no seu bloco de notas, a 31.Março.1876, na qual dizia: “Sirius fotografado. Placa de Wet, 9 minutos de exposição. Fotografia sobre a borda da placa em consequência da deficiência de ajustamento. 3 riscas na parte refrangível do espectro”.
Há aqui também referência às observações de Vénus e da estrela Betelgueuse, no dia 3 de Abril.
Contudo, foi, em 1868, que o casal Huggins conseguiu detectar, pela primeira vez o efeito de Doppler no espectro da estrela Sirius. As riscas espectrais eram quase iguais às do Sol, mas apresentavam um ligeiro desvio. De facto, detectaram um deslocamento na posição da Risca F correspondente a um aumento no comprimento de onda (λ) de 2,2 x 10-4 (0,022%), a que correspondia uma velocidade de afastamento de 66 km/s. Outras fontes falam apenas de 0,015%. Mas, para os nossos cálculos o valor exacto (nenhum era exacto na altura) não é o que mais importa. O importante é perceber como a partir do desvio das riscas espectrais se pode calcular a distância da fonte emissora.
Embora a fórmula original deduzida por Doppler não seja muito prática para aqui aplicarmos, há outras formulações mais simples e fáceis de entender:
Embora a fórmula original deduzida por Doppler não seja muito prática para aqui aplicarmos, há outras formulações mais simples e fáceis de entender:
Vamos fazer as respectivas substituições nesta equação
De acordo com a demonstração de Christian Doppler, o sinal + significa aproximação e o sinal - afastamento.
Portanto, a estrela Sirius, estrela mais brilhante do céu e que se encontra à distância de 8,6 anos-luz, está a afastar-se do Sol à velocidade de 66 km/s. Claro que este número está exagerado; hoje com medidas mais precisas sabe-se que a sua velocidade radial é apenas de - 7,6 km/s.
A partir deste momento, as observações e os número de espectros multiplicaram-se, crescendo exponencialmente em número e em precisão.
Estava aberta a auto-estrada que nos iria levar à evolução do Universo e ao aparecimento do modelo do Big-Bang e de outras tentativas para tentar explicar o mistério (inexplicável) do Universo.
Vamos pois continuar o nosso caminho, agora que já podemos obter dados experimentais. Veremos a que nos conduzem.
Mas os modelos experimentais precisam de suporte em modelos teóricos.
São os nossos capítulo seguintes. Mas o caminho é ainda muito longo.
Por isso temo direito uma pequeno repouso musical.
De acordo com a demonstração de Christian Doppler, o sinal + significa aproximação e o sinal - afastamento.
Portanto, a estrela Sirius, estrela mais brilhante do céu e que se encontra à distância de 8,6 anos-luz, está a afastar-se do Sol à velocidade de 66 km/s. Claro que este número está exagerado; hoje com medidas mais precisas sabe-se que a sua velocidade radial é apenas de - 7,6 km/s.
De qualquer modo, com esta primeira observação, os Huggins mostraram o aspecto verdadeiramente revolucionário da espectroscopia, que iria permitir desvendar milhares de segredos em corpos celestes situados a muitos milhões de quilómetros e sem possibilidade e os podermos analisar in loco.
Além disso, esta simples experiência permitiu tirar as seguintes conclusões:
Além disso, esta simples experiência permitiu tirar as seguintes conclusões:
- é possível medir a velocidade radial das estrelas e não apenas o seu movimento próprio;
- cada estrela é formada por elementos semelhantes aos existentes na Terra, embora deslocados das suas posições originais.
A partir deste momento, as observações e os número de espectros multiplicaram-se, crescendo exponencialmente em número e em precisão.
Estava aberta a auto-estrada que nos iria levar à evolução do Universo e ao aparecimento do modelo do Big-Bang e de outras tentativas para tentar explicar o mistério (inexplicável) do Universo.
Vamos pois continuar o nosso caminho, agora que já podemos obter dados experimentais. Veremos a que nos conduzem.
Mas os modelos experimentais precisam de suporte em modelos teóricos.
São os nossos capítulo seguintes. Mas o caminho é ainda muito longo.
Por isso temo direito uma pequeno repouso musical.
E para terminar ouçamos esta peça da compositora norte-americana Adrienne Albert, nascida em 1941, intitulada "Efeito Doppler". Ela própria conta como lhe surgiu a ideia: "A ideia de escrever uma peça, baseada nas constatações de um matemático austríaco que observou o aumento e a diminuição da altura do som quando a fonte e o observador se aproximavam ou se afastavam, surgiu-me durante uma viagem a Itália, ao ouvir as miríades de sirenes passando pelo meio de um trânsito tão intenso. O motivo (da peça) desce por uma segunda menor, retornando à harmonia original combinada com as segundas menores repetidas, retratando os sons incessantes das buzinas dos carros. As linha smelódicas retratam a vitalidade e a sensualidade das pessoas em contraste com a loucura que se passava em torno delas".
Páginas 1 e 2 da Composição "Doppler Effect" que pode ouvir aqui uma das muitas interpretações.


















Sem comentários:
Enviar um comentário